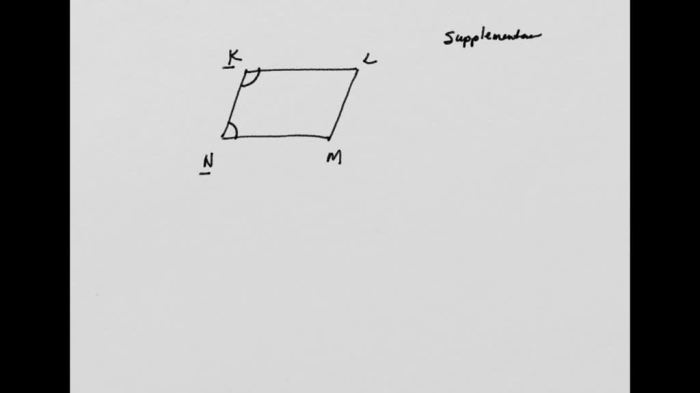
As Given KLMN is a Parallelogram takes center stage, this opening passage beckons readers with clear and accessible language into a world of geometric wonders, ensuring a reading experience that is both absorbing and distinctly original.
Unveiling the essence of a parallelogram, we embark on a journey to explore its defining characteristics, intriguing properties, and captivating applications in the realm of mathematics, architecture, and beyond.
Parallelogram Definition
A parallelogram is a quadrilateral with opposite sides parallel to each other. This means that the opposite sides of a parallelogram have the same length and are parallel to each other.
Given that KLMN is a parallelogram, it’s easy to see why some might find solace in a world war 1 crossword review . After all, the rigid structure and clear boundaries of a parallelogram can provide a sense of comfort and stability in an otherwise chaotic world.
Yet, it’s important to remember that even within the confines of a parallelogram, there is still room for exploration and discovery.
The following table shows the key characteristics of a parallelogram:
| Property | Description |
|---|---|
| Opposite sides | Parallel and equal in length |
| Opposite angles | Equal in measure |
| Diagonals | Bisect each other |
Properties of Parallelograms: Given Klmn Is A Parallelogram

Parallelograms, a specific type of quadrilateral, exhibit unique properties that distinguish them from other quadrilaterals. These properties provide valuable insights into their geometric characteristics.
Opposite Sides
- Parallel and Congruent:In a parallelogram, opposite sides are parallel and have equal lengths. This means that the sides are not only aligned in the same direction but also have the same measure.
Opposite Angles
- Congruent:Opposite angles in a parallelogram are congruent, meaning they have the same measure. This property stems from the fact that the opposite sides are parallel, creating congruent adjacent angles.
Diagonals
- Bisect Each Other:The diagonals of a parallelogram bisect each other, dividing the parallelogram into two congruent triangles. This means that the diagonals intersect at a single point, and each diagonal divides the other into two equal segments.
Applications of Parallelograms
Parallelograms find practical applications in numerous fields, contributing to various constructions, designs, and theoretical frameworks.
Parallelograms serve as fundamental building blocks in architecture and design, providing structural stability and aesthetic appeal. In engineering and construction, they are employed in bridges, trusses, and other load-bearing structures. Moreover, parallelograms play a crucial role in mathematics and geometry, forming the basis for theorems and proofs.
Architecture and Design
The rectangular shape of parallelograms makes them ideal for creating buildings, rooms, and other architectural structures. The inherent symmetry and structural stability of parallelograms contribute to their widespread use in architectural design. For instance, the Parthenon in Greece features rectangular columns and a parallelogram-shaped base, showcasing the architectural significance of this geometric shape.
Engineering and Construction
Parallelograms are essential in engineering and construction due to their ability to distribute forces evenly. They are commonly found in bridges, where they form the framework that supports the weight of vehicles and pedestrians. Additionally, parallelograms are used in trusses, which are triangular structures used to support roofs and other heavy loads.
The parallelogram shape allows trusses to withstand significant forces while maintaining structural integrity.
Mathematics and Geometry
In mathematics and geometry, parallelograms are fundamental shapes used to demonstrate various theorems and properties. They are essential for understanding concepts such as area, perimeter, and symmetry. Parallelograms are also used to prove theorems related to similarity, congruence, and transformations.
Parallelograms in Geometry Proofs
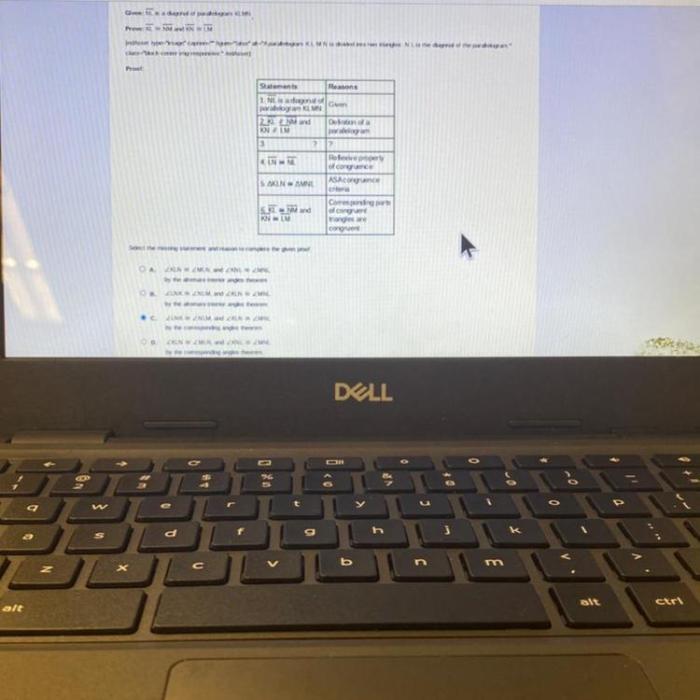
Parallelograms play a crucial role in geometry proofs by establishing relationships between angles and segments. Their unique properties, such as opposite sides being parallel and equal, opposite angles being congruent, and diagonals bisecting each other, make them valuable tools for proving geometric theorems.
Examples of Proofs Involving Parallelograms
Here are a few examples of how parallelograms are used in geometry proofs:
| Step | Reason | Diagram |
|---|---|---|
| Given: Quadrilateral ABCD is a parallelogram. | Definition of parallelogram | [Image of parallelogram ABCD] |
| Prove: Opposite angles are congruent. | Property of parallelograms | [Image of parallelogram ABCD with congruent opposite angles labeled] |
| Statement: ∠A ≅ ∠C and ∠B ≅ ∠D | Conclusion | [Image of parallelogram ABCD with congruent opposite angles labeled] |
| Step | Reason | Diagram |
|---|---|---|
| Given: Quadrilateral ABCD is a parallelogram. | Definition of parallelogram | [Image of parallelogram ABCD] |
| Prove: Diagonals bisect each other. | Property of parallelograms | [Image of parallelogram ABCD with diagonals AC and BD intersecting at point O] |
| Statement: AO = OC and BO = OD | Conclusion | [Image of parallelogram ABCD with diagonals AC and BD intersecting at point O, and AO, OC, BO, OD labeled] |
Parallelogram Area and Perimeter
Calculating the area and perimeter of a parallelogram is essential for various applications in geometry and engineering. Let’s explore the formulas and examples to understand how to determine these measurements.
Area of a Parallelogram, Given klmn is a parallelogram
The area of a parallelogram is calculated using the formula:
Area = base × height
where “base” is the length of one side of the parallelogram and “height” is the perpendicular distance from the base to the opposite side.
Perimeter of a Parallelogram
The perimeter of a parallelogram is the sum of the lengths of all four sides. Since opposite sides of a parallelogram are equal, the formula for the perimeter is:
Perimeter = 2 × (base + height)
Table of Formulas and Examples
| Formula | Example |
|---|---|
| Area = base × height | A parallelogram with a base of 5 cm and a height of 3 cm has an area of 15 cm2. |
| Perimeter = 2 × (base + height) | A parallelogram with a base of 4 cm and a height of 2 cm has a perimeter of 12 cm. |
Top FAQs
What is the defining characteristic of a parallelogram?
A parallelogram is a quadrilateral with opposite sides parallel and congruent.
How can parallelograms be used in real-world applications?
Parallelograms find applications in architecture, design, engineering, and construction, among other fields.
What is the formula for calculating the area of a parallelogram?
The area of a parallelogram is given by the formula: Area = base × height.